Upper left is the classic Poggendorff figure: the oblique lines are objectively aligned, but the upper one appears shifted just a bit to the left. There are lots of variants on this illusion. For example, about forty years ago, researcher Stanley Coren showed that the effect persists, weakly, when the configuration is reduced to dots, as at upper middle. And top right is another variant, the Poggendorff-Without-Parallels: the misalignment effect persists, weakly, in two objectively aligned segments even without the long parallel inducing lines. Most researchers have found that this last effect is greatest when the test arms are at an angle of around 22 degrees from vertical. An analogous affect shows up when they are rotated the same amount form horizontal.
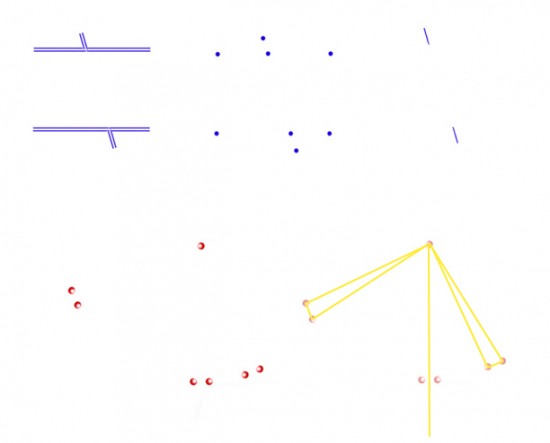
To my eye, the Poggendorff-Without-Parallels effect even appears when the little test line segments are reduced just to dots, as shown lower left. Imagine joining up each of the three pairs of dots with the isolated dot, so that we end up with three triangles. If we then drop a vertical line from the isolated dot to the middle pair of dots, it will pass through the mid-point in between them, as diagrammed in yellow to the right. So the middle triangle of dots has sides of equal length, or is equilateral, as the geometers call it, and that’s just how it looks. No surprises so far. But now here’s the interesting bit. The two other triangles of dots, rotated respectively clockwise and anti-clockwise from vertical, remain objectively equilateral, but that’s not how I see them. For me they now look more like right-angles triangles, as diagrammed with yellow lines to the right. The effect suggests a shift in apparent position of the right hand pair of dots, (rotated anti-clockwise about 22 degrees from vertical), just about equivalent to the shift we seem to see in the Poggendorff-Without-Parallels, shown above it at top right. There’s an equivalent shift for me in the pair of dots rotated around 22 degrees from horizontal.
It would be really useful to have comments on whether that works for you, or whether for you the rotated dot arrays still present equilateral triangle arrangements. Illusions like these often do look different to different observers, and it’s also all to easy, once you have a theory about what’s going on, to see things the way your theory says they should look.
11 June 2012: This is a revision of the original post. It included a 3D demo of the dotty effect, but with triangles of dots that turned out not to be truly equilateral…. Woops.
