This is an animation of Shepard’s Tables, an illusion first published by Roger Shepard as Turning the Tables, (see his wonderful book Mind Sights, 1990, pages 48 and 127-8). The left hand lozenge-shaped table top seems to get longer and thinner as it rotates, but it’s an illusion. It remains identical to the right hand table-top, except for rotation. The table-tops look even more different as the legs appear. The illusion is an example of size-constancy expansion – the illusory expansion of space with apparent distance. The receding edges of the tables are seen as if stretched into depth. Earlier posts on size-constancy showed how objects can appear wider with distance. That shows up with Shepard’s tables too, in the way that the oblique edges of the tables seem to get a bit wider apart with distance. The stretch into depth is more striking.
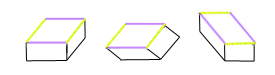
Recently Lydia Maniatis pointed out a puzzling aspect of the illusion, in her prize-winning entry for the Illusion of the Year Competition. Here’s a version of her figure.
All three table tops are identical, but the middle one looks different from the one on the left, though it’s not even rotated. Instead the vertical axis of the figure is shown at an angle to gravitational vertical. That means that the blue edges are no longer aligned with the frontal plane of the image, as to the left, even though they are horizontal on the page, but must be receding into distance. And yet we don’t see the dramatic stretch into depth that appears with oblique edges that recede into distance. Why not? Try looking at the middle block with your head leaning over to the left, so that the short edges are aligned with your head, and therefore with the vertical axis of your field of view. Now (for me) the blue edges do stretch into depth, though not as much as in the right hand image viewed normally.
What do you think is going on? I’ll take a shot at an explanation in a post in a couple of days.

It is easy to see the difference in the animation but hard to understand the principle below the animation.