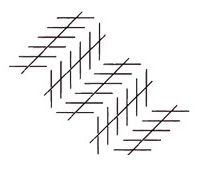
Here’s a rather subtle effect. It’s a competition underway, when the Zollner illusion is seen embedded in a staircase. In the staircase lower left, where two of the long lines are either side of the outside edge of a step (in other words like lines a and b here, on the sides of a convex step), the lines seem to get further apart with distance, as they would in a normal presentation of the Zollner illusion. But wherever on that lower left stair the lines are like b and c here, either side of the inner edge of a step, (so on a concave step), they tend to look much more parallel. In a normal version of the illusion, as below, the equivalent long lines appear to get closer together to the right.
Want to know more?
The Zollner illusion is still a bit of a mystery, but what seems to be happening in the stair version is that the pattern characteristics that usually cause the Zollner effect are being either enhanced or suppressed by the size-constancy effect. When the long test lines lie either side of an outside step edge, both the Zollner and the size-constancy effect work together to make them seem wider apart with distance. But either side of an inside stair edge, like lines b and c in the lower left stair, the Zollner effect is making the lines seem to get closer together with distance, in competition with the size-constancy effect, which makes them diverge.
Now check out lines b and c in the stair upper right, which we see from below. (That’s still in the big pic at the start of the post). Here convex and concave have swapped. Lines b and c now flank an outer edge of the step, and so the Zollner and size constancy effects are working together again to make the lines wider apart with distance, instead of pretty much parallel
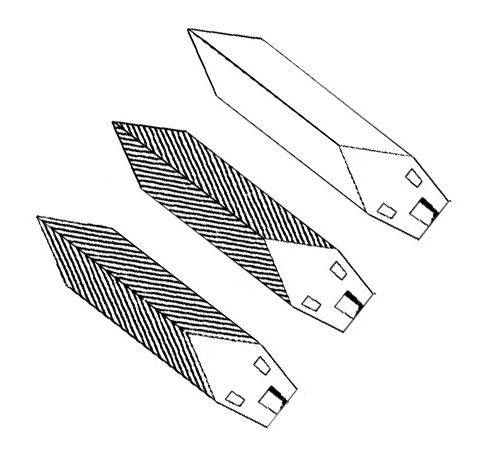
In support of the idea that there’s a competition involved, check out the little houses, below. In the upper right house, just the size-constancy effect is at work, and the edges of the roof seem to diverge with distance. In the lower left house, that’s in agreement with a Zollner type effect, also acting on the outer edges of the roof, so they diverge even more strongly. But in the middle house I’ve reversed the direction of the striations. Now there’s a competition and the Zollner effect has pretty much balanced the size constancy effect, so that (to my eye) the roof edges are about parallel – maybe just converging a little, to the left.
I wrote a scientific paper about this, but here’s my chance to put the record straight on point of priority. When I wrote my paper, I hadn’t realised that this competition effect had already been written up by someone else, decades earlier. For the record, the prior paper was by H.J.Jeffrey, An Inquiry Into Inappropriate Constancy Scaling, in the Quarterly Journal of Experimental Psychology, vol 20, pages 294-6, back in 1968.