Like our bubble pictures this is not really an illusion, but I am fascinated by natural shapes. It’s a picture of blades of ice, and what you see here is about three inches across. The colours come from taking the picture in polarised light, as the crystal blades were forming in a shallow dish of water in a freezer.
Want to try your own pictures? The preparations are not trivial, but there’s nothing a school science section couldn’t handle.
My fourth set of small optical illusion and visual perception related images you can link to from your own website / profile page.
In case you missed them you can still see the third set of illusion pictures, the second perception pictures as well as the first set of illusion pictures.
Does Big Ben look like it’s leaning over more in the right hand image than in the left hand one? It can take a double-take to spot that the two pictures are identical. I find it a fantastically strong illusion.
It’s a demo of a new illusion found by Frederick Kingdom and colleagues (you’ll need to scroll down that link to get to their bit – look out for an even more than usual Leaning Tower of Pisa). Their discovery is a new version of the size-constancy illusion. This is my second demonstration of it – a few posts back I used a picture of a historic streetlamp. But here’s an example that looks stronger to me, with a better known subject.
Update 10 Oct 2011. Big Ben really is leaning over! But not (yet) as much as it appears to lean in this illusion.
You probably know the tiling patterns of M.C.Escher. But how about Koloman Moser? Here are a couple of his designs.
Moser was working in Vienna, Austria, a hundred years ago. (He died in 1918). I don’t know where he would have learned to do tessellating designs, that is, designs with motifs that repeat the way jigsaw puzzle pieces fit together, with no gaps or overlaps. If you have checked out our tessellation tutorial, you’ll know that the secret of these designs is that the edge of each “tile” of the pattern must be able to be snipped into pairs of identical line segments. Here’s how it works with Moser’s fish design.
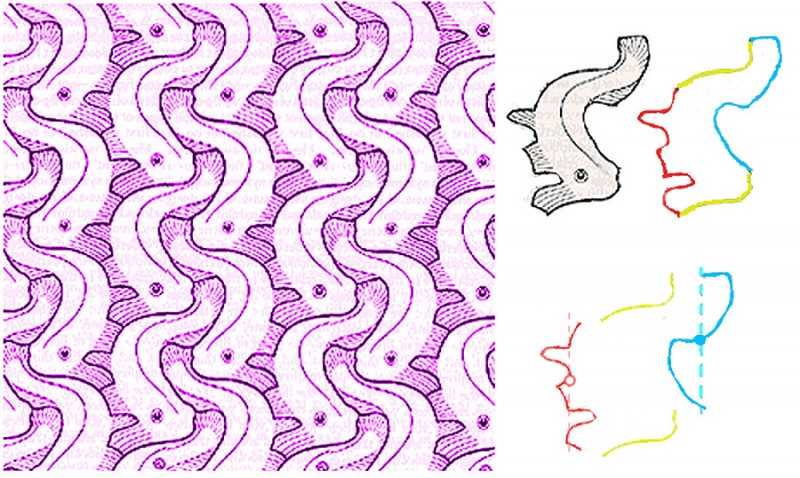
To the right you can see that the fish outline can be divided into three pairs of segments, a yellow pair, a red pair and a blue pair. In the yellow pair, the top line is just repeated lower down to make the pair, in a move called a translation. The red and blue pairs are a bit more complicated. In each pair, the lower line segment is a mirror reflection of the upper segment, but shifted downwards. That kind of shifted reflection is called a glide reflection. It’s a fact that any motif whose edges can be snipped into one pair of segments that repeat by translation, connected as here to two parallel pairs whose edges repeat by glide reflection, will tessellate perfectly. And that’s just one of 28 recipes for motifs that tessellate.
For a more technical account of Moser’s symmetry designs, see:
https://archive.bridgesmathart.org/2019/bridges2019-411.pdf
The author (John M.Sullivan of the Technische Universität Berlin) analyses numerous Moser designs, including the right hand design in the image at the start of the post. He points out that, in an earlier version of this post, I got the analysis of this fascinatingly complex design wrong.
