Tessellations are patterns whose repeat motifs fit together like jig-saw pieces, with no gaps and no repeats.  For an introduction, see our earlier animation. They can be abstract patterns, but the most intriguing are the ones devised by tessellation maestro M.C.Escher in the middle of the last century, which show representational motifs, such as animals, as tessellating patterns.

Designing abstract patterns that tessellate successfully is just a matter of getting the hang of some rules.  Discovering representational motifs that tessellate is much, much harder.  There are no procedures, or none that I know anyway.  It’s all trial and error, mostly error for me, and really hard!  Escher was brilliant at it.  My efforts are pretty feeble.

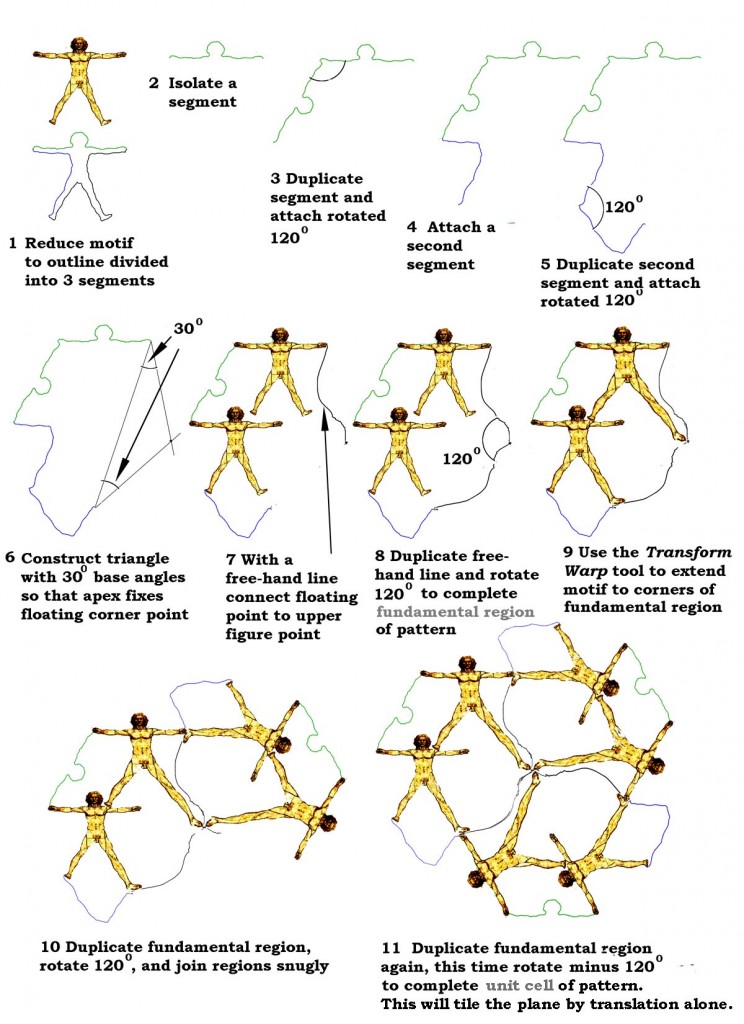
But fortunately, you can at least include representational motifs within your tessellations with a little trickery.  The pattern above, based on Leonardo’s famous Vitruvian Man, is an example.  The secret is to use segments of the outline of the representational motif for part of the outline of the tessellating pattern cell.

You do need to be up to speed with making abstract tessellations, and also pretty expert with Photoshop or an equivalent graphics package.  But if you’ve reached that point, or are just curious, here are stages in the development of the pattern shown above….

 

 

As you will know if you have looked at our tessellation tutorial, or are already an expert, there are 28 recipes for motifs that will tessellate.  For this design I chose one known as Heesch H9.  For this recipe, each cell, or fundamental region, of the pattern has a boundary made up from three pairs of segments. The segments in each pair are identical, and they’re connected so that if they were rotated until one overlaid the other, they would exactly coincide.  To connect them so that they form part of the boundary of a Heesch H9 cell, imagine them overlapping like that first, and then, keeping one end of the pair aligned, rotate one segment of through 120 degrees, as when the minute hand of an old fashioned clock face rotates from 12 oclock to about 8 0clock. The boundary of the whole cell consists of three pairs of segments like that, measuring the 120 degree angle inside the cell.

It’s still quite hard to end up with a satisfying tessellation.  All too easily, your chosen representational element overlaps the boundaries of the cells, and it’s also very easy to accidentally connect up the segments the wrong way, or get the angles wrong, so that the cell you end up with won’t tessellate.  I haven’t yet found any guidelines other than trial and error – though I’m sure there must be some.

I’ve used one other trick here.  At stage 9, I’ve distorted Leonardo’s beautiful drawing to extend one leg of each figure so that it makes contact with one of the points where boundary segments meet.  That adds a whole new set of connections and centres of rotation to the pattern, which I reckon makes it more complex and fascinating.