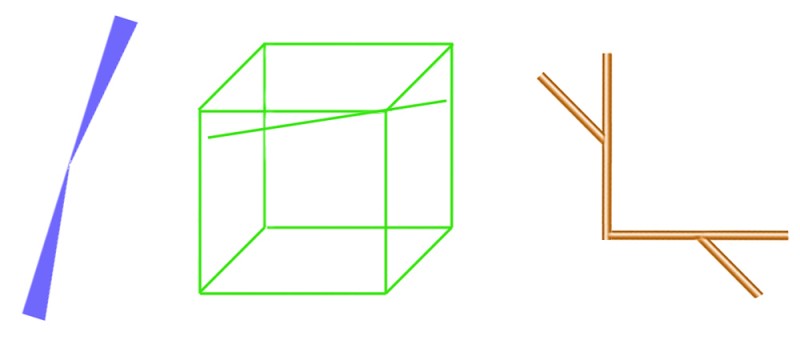
Here are three rather subtle illusions, each showing bent lines. In Bourdon’s illusion, to the left, the straight left hand edge looks bent. In Humphrey’s figure, centre, the straight, loose line touching the corner of the cube looks bent. And in the figure to the right, the straight line interrupted by the corner looks bent. I don’t think we really understand any of these illusions, and they are not very dramatic, so you don’t see them often. When someone does puzzle them out, for sure they’ll be a key to subtle ways the brain works. There’s probably a different explanation for each. For example, both the left and middle figures show a bent line that is the backbone of two triangles meeting at a point, so you might think, hello hello, we’re getting somewhere. But then you notice that the lines bend in different directions in relation to the triangles each illusion.

If you like to tangle with the technicalities, there are learned studies of the Bourdon illusion and the corner figure, though unfortunately, you’ll only get an abstract of the articles on those links, unless you are in a university library where they subscribe to the journals. And you won’t find much on Humphrey’s figure anyway, it’s seriously obscure.

Here’s a bit more on the corner figure  ….

 

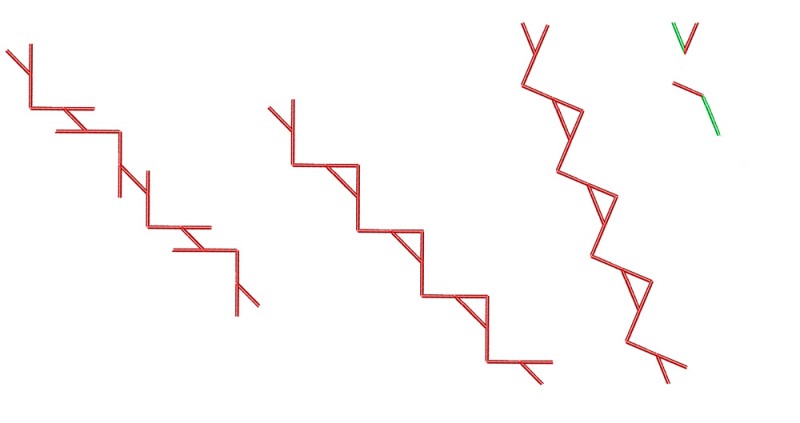
Here I’ve chained the figure, to see whether I can amplify the illusion (left) and cancel it (centre).  On the left, reversing the triangles means that the ones flanking each segment of test line are collaborating so as to rotate the segment in the same direction.  Take the segment between the upper two arrowheads. The upper arrowhead is making it seem to rotate clockwise.  But then so is the next arrowhead down.  Now check out the middle segment.  Its flanking arrowheads are collaborating to rotate it anti-clockwise.  As a result, the illusion gets a bit of a boost and the line of little test segments has a slight, whacky zig-zag to it.  But then in the middle the triangles are acting on the segments in between them in competition (if you think about it for a moment – now the top arrowhead is still making the segment below it rotate clockwise, but the next arrowhead down is making the very same segment rotate anti-clockwise). So the illusion is cancelled by the competition and the middle three segments look aligned, with just the loose end lines a bit rotated.

But then towards the right, at a steeper angle, it gets complicated. The three middle test segments still look to me parallel, but slightly skew, so they’re parallel but don’t line up. That’s because at this orientation another illusion comes into play, the Poggendorff illusion. However, here it’s an unusual version of Poggendorff, because the misalignment appears between objectively aligned arms of two different kinds of angle, as top right. Note that this figure is just the corner figure as immediately to the left, but with most of it chopped off. In the technical literature this is called amputation. Not very nice.  But it is often the case, as here, that you have a really complicated figure, and actually when you chop off all the bits that don’t affect the illusion it’s not quite so mysterious. Mind you, there’s no agreement about:

how the Poggendorff illusion works;

whether my figure top right is really the same illusion;

whether the effects observed in the figures to the left play any role in the Poggendorff illusion.