One of the most obstinately puzzling illusions is Poggendorff’s, in which a slanting line interrupted by a gap no longer looks aligned. For over a century specialists have been unable even to agree whether it arises from 2D properties of the image, or as a result of attempts by the brain to interpret the configuration as 3D. Papers written a hundred years ago treat the problem in very much the same terms as we do today. I’m betting on 2D (I argue for that on another, website devoted to the Poggendorff illusion). It’s not likely my speculations are spot on, and they may well not even be in the right direction. But read on here if you’d like to see demonstrations that show why I don’t think depth processing can be the answer.

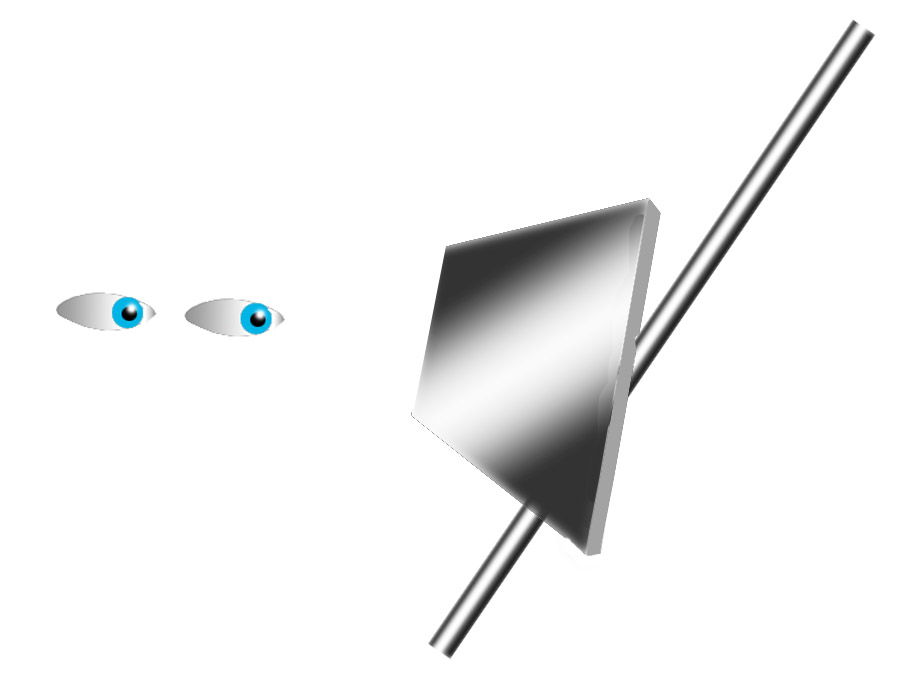
First, what’s the case in favor of depth processing as the source of the misalignment?  It starts from the assumption that any oblique line in the visual field is interpreted early in visual processing as probably receding away from the viewer. However, the argument goes, the brain does not necessarily interpret the interrupted oblique lines in Poggendorff figures as continuous in space, for example as if they were inscribed on a receding surface, as to the left in the picture at the start of the post. More probably, the oblique lines might be discontinuous, like the centre and right hand lines in the picture.  If this were a real scene, those lines would be laterally and vertically displaced from one another in space. They could only appear aligned because of an accident of viewpoint. On that assumption the misalignment in Poggendorff figures arises, some believe, because our brains make an adjustment for assumed spatial displacement in the test obliques.

Others suggest that the interrupting lines are seen as edges of a surface, blocking our view of a line, which is continuous, but which lies at a different orientation in space from the occluding surface.  That is shown below as if seen from the side:

As a result, the argument goes, the brain is not sure exactly how far away the junctions between the oblique line and the edges of the interrupting rectangle are.  Is the upper junction, for example, where it would be on the oblique line, or only as far away as the interrupting edge?  Apparent misalignment might arise from the depth confusion, for example because apparent position as seen in one eye might then be expected by the brain to be different from position as seen by the other.

On the face of it these accounts sound very plausible. My problem with them is that it seems to me that the illusion can arise vividly when the Poggendorff figure is explicitly inscribed within a surface, so that there’s no scope for confusion about lateral or vertical displacement. However, just showing the test lines confined to a continuous surface in a picture, as to the left in the picture with the poultry at the start of the post, isn’t enough. It takes the brain a large fraction of a second to decide that a picture like that is of Poggendorff figures on an odd-shaped block  (a fifth of a second or so). Before the decision is made, the image may evoke alternative preliminary hypotheses about possible spatial orientations of the Poggendorff test lines. Illusion might arise just from those initial assumptions  Even once the left hand test obliques on the block in the picture are seen as lying within a plane, illusion might linger like a ghost of the discarded hypothesis.

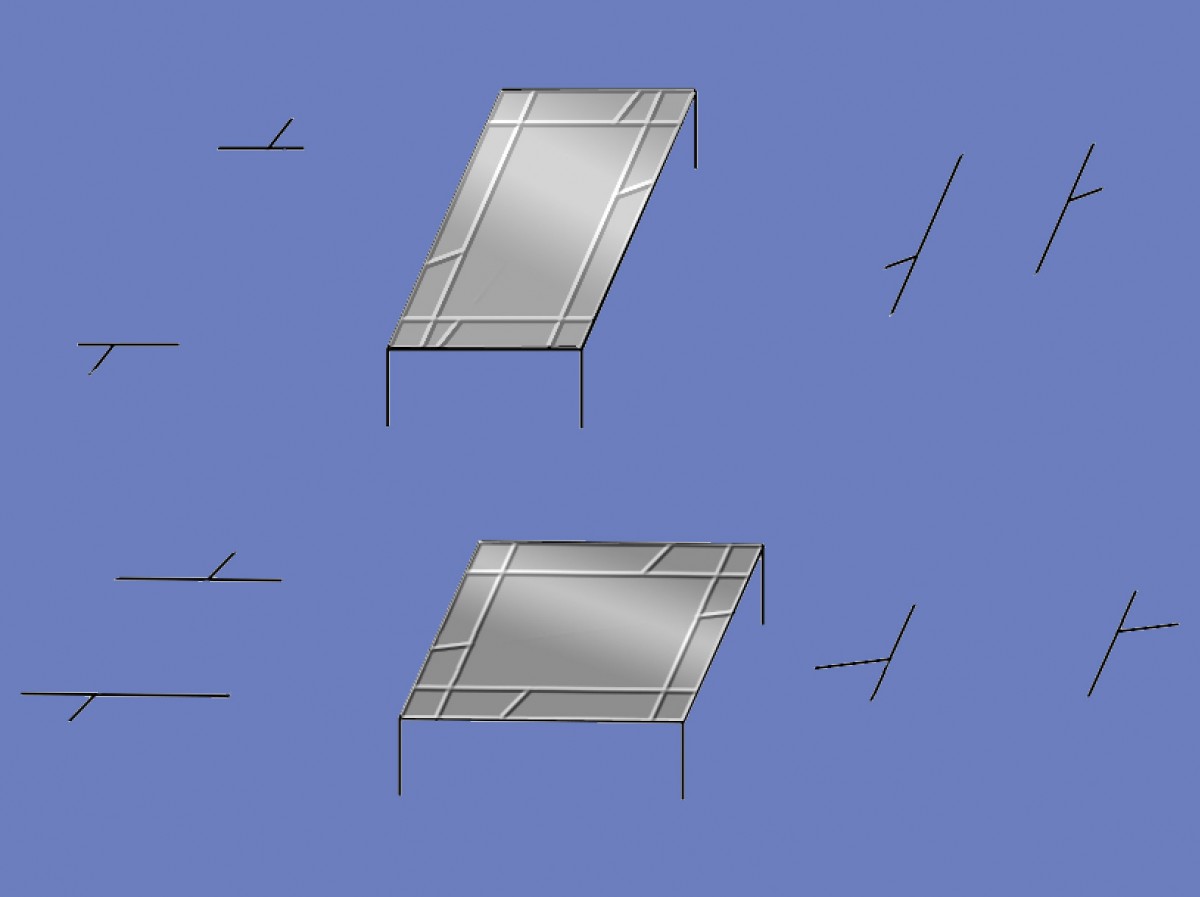
But check out this picture:

What I’ve done is to embed some Poggendorff figures in another illusion, Shepard’s tables. This is an amazing illusion. The two tabletops are identical, but it can be hard to believe, unless you measure them just as parallelograms on the screen. One presents its short side head on to us, and the other its long side, that’s all. As with the previous image of a table, the culprit is the size-constancy effect, but this time we see not just divergence of the oblique edges of the tables, but a dramatic stretch-into-depth with distance.  So we see one table as squat, the other as long and thin.

Here’s the key point for us:  we know that this kind of spatial scheme, with the flat table tops receding into depth, seems to be established very early in visual processing. (See the earlier post about paradoxical size-constancy). Could the oblique lines in the Poggendorff figures on the tabletops be evoking a quite different spatial scheme, as required by most depth processing theories of these illusions, indicating that the lines may not be confined to the surfaces?

In principle, maybe. It could be that very early in processing, every possible spatial configuration of an array of geometric lines is, as it were, put on stand-by, and that all but one possibility is then eliminated (very rapidly) in a sort of Darwinian process of selection of the most probable. If so, it could be argued that illusion could arise even from a configuration that survives as a possibility only for a moment. I suspect that a process of elimination of possibilities like that could indeed go on. I find it much less likely that in the process two quite separate illusions, the effects associated with Shepard’s tables on the one hand, and Poggendorff effects due to lateral or vertical displacement of the test lines on the other, could both survive the selection process. The Poggendorff misalignments here seem unequivocally inscribed in the table-tops, along with size-constancy effects, very early on in visual processing. And yet the misalignments, to my eye, are just as strong as in the bare reference figures either side of the tables – the three D context is making no difference.

However, there is one other theory attributing the Poggendorff illusion to depth processing that would not be challenged by inscribing the lines in Shepards table-tops.  It could be that the misalignment we observe simply arises from the size-constancy effect alone.  That effect can make space seem to expand with distance.  It gives rise to the apparent stretch-into-depth of Shepard’s tabletops, and in the image below to the illusory divergence of the oblique table edges, which are objectively parallel.  So maybe, it is argued, either an illusory stretch-into-depth, or the apparent table edge divergence, is also acting on the oblique test lines in Poggendorff illusions.

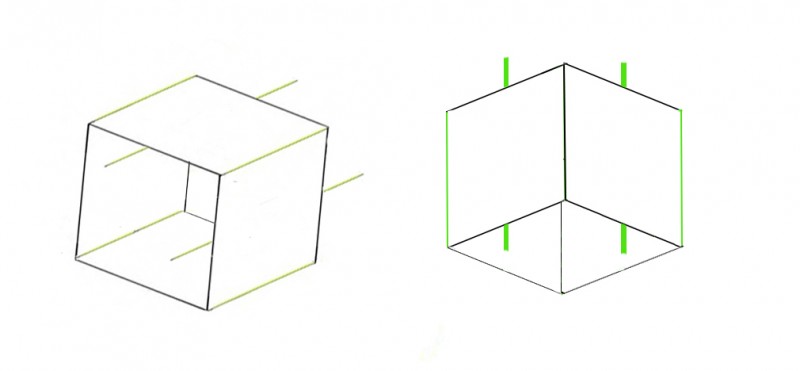
But then what about this next picture?  (Added at 28 July 2013).

The yellow, outer edges of the open-ended boxes appear to fan out with distance, so that their far ends seem further apart than their near ends.  That is, with nearer ends to the left in the cube on the left and at the bottom in the cube to the right.  But now note that although the oblique Poggendorff test lines appear to agree with that as far as orientation goes, the Poggendorff effect acts in opposition, so that in each cube the two distant test line segments appear closer together than the two near test line segments.  That’s not consistent with an apparent expansion of space with distance as the cause of the Poggendorff effect.  It just might be argued that in the cube to the left, it would be consistent if we imagine that size-constancy effects act in separate horizontal and vertical registers.  But the persistence of the effect in the right hand cube rules that out.  The most probable interpretation, for me, is that spatial constancy scaling and Poggendorff effects arise from completely different processes.

In further support of that, consider this next picture too.

This time I’ve embedded a Poggendorff figure in the Ponzo illusion. Once again, the context presents depth unequivocally, complete with the kinds of size-constancy changes that we know arise early in visual processing. The distant woman, objectively the same size as her sisters, looks larger. There is also to my eye some divergence in the oblique edges of the parallelogram, although in this picture the oblique edges don’t seem to stretch into depth unequivocally in the way they do in Shepard’s tables – it’s not really obvious that the parallelogram is horizontal rather than vertical in the field of view.  But even if we see the parallelogram as receding in space, when the Poggendorff test arms are presented laterally there seems little scope for distance to be involved, because the junctions of the test arms and the parallels are not far off equidistant from our viewpoint. Once again, some will argue that very early in processing other spatial configurations are briefly in play, and that Poggendorff effects might arise, as it were like ghosts, left over from these rapidly discarded possibilities.  But would the brain really discard one hypothesis about spatial arrangement in favour of another so early in processing, and still retain illusions arising from the first hypothesis?

Another argument in support of various depth processing accounts of the Poggendorff illusion is that when we see a Poggendorff configuration in a stereo image, but arranged so that the interrupting rectangle appears as a panel in front of a continuous rod, illusion is reduced or vanishes. That might indeed be expected if the configuration we see in 3D suppressed the hypothetical spatial arrangements that are supposed to give rise to misalignment in early processing. But is effect reduced in the stereo pair below?  (You won’t be able to see this as a 3D image unless you have the knack of viewing stereo picture pairs without a special viewer, in the mode known as cross-eyed viewing. If you need some practice, try this tutorial). To my eye, seen in 3D the panel is now floating in front of the rod. The Poggendorff effect seems to be little reduced if at all.

And even when I rig up a real set-up at home, with some kind of panel blocking my view of an oblique broomstick a few inches behind it, I still see the broomstick as misaligned.  I think there can be some reduction in illusion in the 3D views.  However  I suspect that in these cases any reduction in illusion could be because the Poggendorff effect, caused by physiological processes early in the visual pathway, is inhibited to an extent by our knowledge that the rod is continuous.  That is, the misalignment effect arises early in processing, from two-dimensional scene properties, but is then inhibited by depth processing, rather than caused by it, because our experience indicates that the rods as seen in 3D are probably continuous.

Update May 2012! I’ve now added a new stereo demo of a real backyard lash-up of the Poggendorff illusion in 3D,

I reckon Poggendorff must be a 2D thing. I do agree that 3D context can enhance or suppress the effect. As another example, in the picture with the poultry at the start of the post, the left hand, surface-bound line sometimes looks to me less misaligned than the centre and right hand lines. For me, that would once again be because we’ve decided that, in this particular case, the oblique test lines are the ends of a continuous line on a surface.  Our brains the reduce the illusion, updating the assumptions arising in early processing in the light of our knowledge that in these cases the test lines are continuous. However the illusion still wins out. Thanks to whatever 2D characteristics of the figures produce the illusion, some misalignment persists.

Still, the brain is fabulously subtle. I wouldn’t be too dogmatic about this 2D/3D thing, not yet.  And there’s one study that poses a real challenge for any 2D account.  Qin Yang and Masanori Idesawa showed that when the illusion is seen in 3D but with the test arms in from of the inducing parallelogram, illusion vanishes.  That’s a tough one.