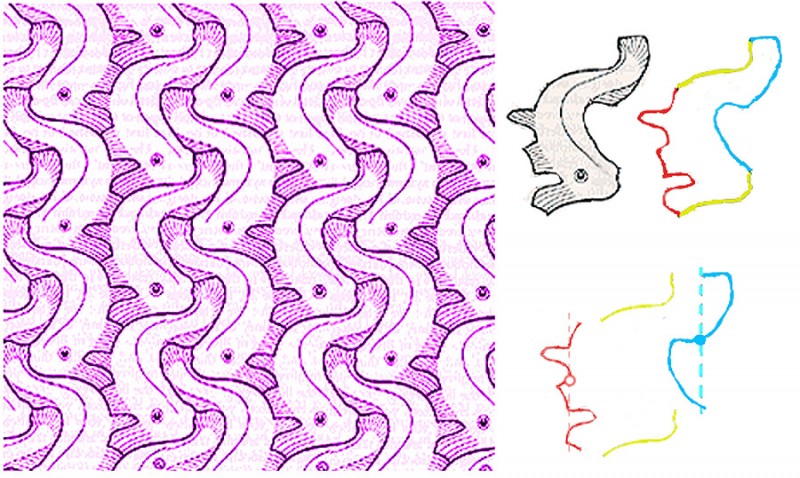
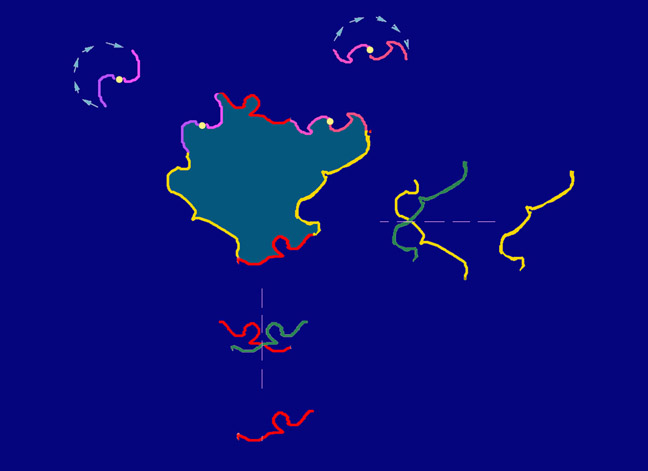
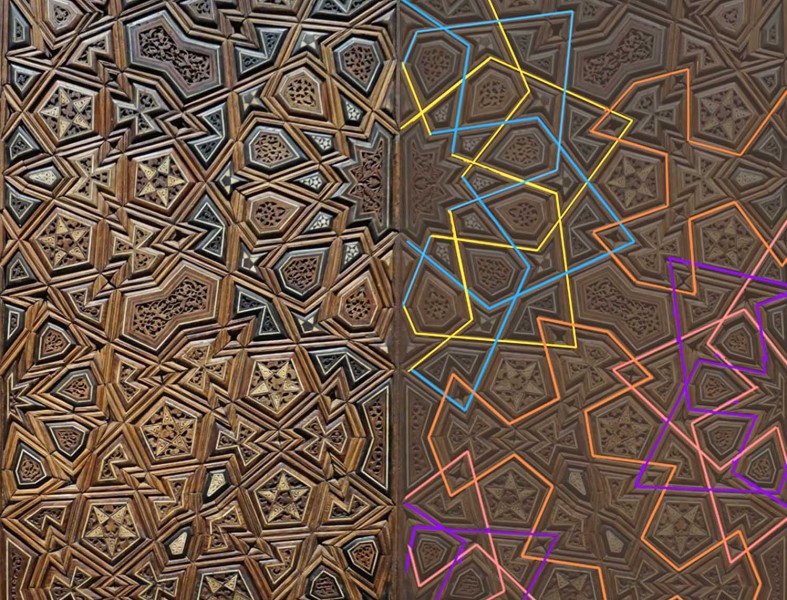Category Archives: Tessellations

Ambiguous images, Illusion demos with animations, illusions and aesthetics, Optical Illusions, Tessellations

Digital Kaleidoscopes – post no. 1

Everyone loves a kaleidoscope, particularly the ones with a lens at the end, so that as you look through them whilst sweeping the kaleidoscope around, the view becomes a dazzling starburst pattern.  (I find Nova Magic Marble kaleidoscopes are inexpensive ones for kids that work pretty well).   However, real-world kaleidoscopes can only tile the visual field with a limited repertoire of geometric shapes – typically triangles. Digitally we can tile with any shape that will tessellate – that is, fill the plane by repetition without gaps or overlaps. As with real-world kaleidoscopes with a lens at the end, each tile can enclose a streaming segment of a visual scene, if you are handy with graphics and 2D animation packages.  If that all sounds a bit puzzling, I think the movie will make it clearer.

But then there’s a surprise!  Illusions of movement may appear, dependent on figure/ground effects.

Continue reading →

illusions and aesthetics, Tessellations

Mamluk Interlace

MamlukPair

I’m fascinated by the way that spectacular aesthetic effects often seem to involve bamboozling our everyday strategies for making visual sense of the world.  This is a beautiful example, a detail of interlace decoration on a 14th century (Western dates) Mamluk Period door in the Louvre from the Al-Maridani mosque in Cairo.  (I’ve shown other examples of a role for bamboozled perception in aesthetics in an earlier post, and in the Illusions and Aesthetics category to the right).

As you can begin to see in the image, where I’ve combined the interlace pattern on the door with a schematic analysis of its reflection, the interlace we see in the door is a segment of a rosette pattern that repeats across a wider field.  But that’s not obvious at all when you just see the door.  The artist has not emphasised the lines of the design, but rather the infills – stars and other little geometric tiles.  We’re distracted from grasping the overall geometry by all the assertive, enclosed shapes, with their heavy outlines.  And the overall shapes that do jump out for me are the beautiful curves that run from top to bottom of the image, which also distract attention from the hexagonal geometry of the pattern.  For more analysis of the pattern and the fabrication of the doors, see below, but first, here’s the whole door.

Mamluk Door

Continue reading →

illusions and aesthetics, Tessellations

Cheating with tessellations

Tessellations are patterns whose repeat motifs fit together like jig-saw pieces, with no gaps and no repeats.  For an introduction, see our earlier animation. They can be abstract patterns, but the most intriguing are the ones devised by tessellation maestro M.C.Escher in the middle of the last century, which show representational motifs, such as animals, as tessellating patterns.

Designing abstract patterns that tessellate successfully is just a matter of getting the hang of some rules.  Discovering representational motifs that tessellate is much, much harder.  There are no procedures, or none that I know anyway.  It’s all trial and error, mostly error for me, and really hard!  Escher was brilliant at it.  My efforts are pretty feeble.

But fortunately, you can at least include representational motifs within your tessellations with a little trickery.  The pattern above, based on Leonardo’s famous Vitruvian Man, is an example.  The secret is to use segments of the outline of the representational motif for part of the outline of the tessellating pattern cell.

You do need to be up to speed with making abstract tessellations, and also pretty expert with Photoshop or an equivalent graphics package.  But if you’ve reached that point, or are just curious, here are stages in the development of the pattern shown above….

 

Continue reading →

Animated Illusion Cartoons, Optical Illusions, Tessellations

Animated Illusion Cartoons – re-posting of Chicken and Leaf

Woops, slight technical glitch with the original post of this, just before Christmas. So this is a re-posting of the third of our animated illusion cartoons, Chicken and Leaf. It may still run jerkily on first run through, should be OK second time around.

These cartoons are meant to work just like movie versions of a three- or four-frame cartoon in a newspaper – each one presents a situation that ends with a punch-line.  The cast of characters are all illusion figures of different kinds, but each cartoon depends on a particular illusion effect.

The main illusion effects to watch out for in this movie are tessellations, and especially the final transformation, which transforms across the image at the same time as it transforms locally:

You can also view Chicken and Leaf as a
Quicktime Movie

You can also see our this cartoon along with the previous ones in our Animated Illusion Cartoon category.

I’m fascinated by the effect that the movie ends with – a tessellation that transforms in space and in time. Tessellation (or tiling) wizard M.C.Escher was brilliant at these transforming patterns, as in his Metamorphosis prints, but of course couldn’t do animations.  I’m sure he’d have done the animations if he could, but without a computer they’d have taken years. In my animation there are two sequences of transformations, first where the pattern morphs in sync all over the screen – a number of people have done those – and then the one that morphs across the image as well as in time.  I’m not aware anyone else has done one of those.  Please let me know if so, I’d love to see it – and otherwise, I hope if you’re an animator you’ll be provoked into doing a better one than mine.

Illusion demos with animations, illusions and aesthetics, Tessellations

How to do tessellations – animated demo

LaidBackCatTessellation

Just about our first post was a tessellation tutorial. It was quite comprehensive, but a bit heavy going. I’ve been wanting to post an animated demo, because I reckon that seeing that first would make the tutorial much easier to follow. So the animation is below, but first, a reminder of the basics:

A tessellation is a pattern like the one above. The cells of the pattern fit together like jig-saw pieces, with no gaps and no overlaps. You can’t make a pattern like that out of just any old shape. It only works with shapes whose edges can be snipped into pairs of segments with special properties. The two segments in each pair must be indentical, except that they may be either reflections of one another, or rotated in relation to one another, like the hands of an old-fashioned clock. Confused already? Just watch this animation, showing the evolution of the pattern above, and you’ll see how it all works.

Continue reading →

illusions and aesthetics, Optical Illusions, Tessellations

A tessellation pioneer

4 Comments

You probably know the tiling patterns of M.C.Escher.  But how about Koloman Moser?  Here are a couple of his designs.

Moser tilings

Moser was working in Vienna, Austria, a hundred years ago.  (He died in 1918).  I don’t know where he would have learned to do tessellating designs, that is, designs with motifs that repeat the way jigsaw puzzle pieces fit together, with no gaps or overlaps.  If you have checked out our tessellation tutorial, you’ll know that the secret of these designs is that the edge of each “tile” of the pattern must be able to be snipped into pairs of identical line segments.  Here’s how it works with Moser’s fish design.

Moser design demo

To the right you can see that the fish outline can be divided into three pairs of segments, a yellow pair, a red pair and a blue pair.  In the yellow pair, the top line is just repeated lower down to make the pair, in a move called a translation.  The red and blue pairs are a bit more complicated.  In each pair, the lower line segment is a mirror reflection of the upper segment, but shifted downwards.  That kind of shifted reflection is called a glide reflection.  It’s a fact that any motif whose edges can be snipped into one pair of segments that repeat by translation, connected as here to two parallel pairs whose edges repeat by glide reflection, will tessellate perfectly.  And that’s just one of 28 recipes for motifs that tessellate.

For a more technical account of Moser’s symmetry designs, see:

https://archive.bridgesmathart.org/2019/bridges2019-411.pdf

The author (John M.Sullivan of the Technische Universität Berlin) analyses numerous Moser designs, including the right hand design in the image at the start of the post.  He points out that, in an earlier version of this post, I got the analysis of this fascinatingly complex design wrong.

Illusion demos with animations, Tessellations

Tessellation Animation

2 Comments

The Dutch tessellation whizz M.C.Escher was fascinated by transformations from one tessellation to another, for example in his series of prints Metamorphosis. I’m sure he would have explored animated versions if it had been practical in the 1940’s. So I’ve borrowed a couple of his motifs and animated them. I showed an animated transformation in an earlier post, but that was between two designs that shared the same kind of symmetry. (See the earlier tessellation tutorial for how these tessellations work. If you like technical detail, my earlier animation was of two motifs based on Heesch tessellation no. 11). Sticking to just that one kind of tessellation meant that the corners of each cell of the design had to remain stationary, and only the edges of the cells transformed. This new transformation is a bit different, because it’s not just a transformation from one motif to another, but between two different kinds of symmetry pattern – Heesch nos 17 and 18 in the tutorial – and the corners of the cells of the pattern are not fixed.

In the earlier transforming animation, the design transformed in space, across the image, as well as transforming in time. If I’ve got it right, (I’m not 100% sure about this), that kind of time plus space transformation is not possible in an animation if the corners of the cells of the tessellation change position, as in my new tessellation above. So in this new animation, there’s no change from cell to cell across the design, and all the cells transform together.

I’m fascinated by the artistic possibilities of these kinds of animation, and one aspect of it is to do with what you might call the dance rhythms of the animation. Here’s a variation on the new animation, speeded up and with an added wave that gives a quite different kind of pulse to the design.

These animations are bit monochrome for the moment – colour is on the way, but I’m on a steep learning curve with file sizes, compression etc.

Tessellations

Tessellations with figures

A tessellation is a pattern made up of elements that repeat with no gaps and no overlaps.  The elements may be abstract shapes, or may be recognisable objects or creatures, like the ones in the tessellations of M.C.Escher.  When I begun playing around with tessellations, I thought understanding the procedures needed to make patterns that tessellate would be the hard part.  I thought it would be fairly easy to find creatures in whatever shapes I ended up with.  Not so.  The procedures aren’t so hard.  But fitting creatures into them I found really difficult.  Here’s one of my first attempts.  I started with one of the most complicated recipes for a tessellation.  

 
 

For the details of the procedures, which give shapes that tessellate, see my tessellation tutorial. Essentially, the boundary of every shape that will tessellate is made up of pairs of lines. Within each pair, an identical line repeats, either by rotation, reflection, or just by shifting over. In the example above, there are four pairs of lines, two of them with rotations and two with reflections.

But what creature could I discover in this shape? Here’s what I came up with, a cross between an elephant and a rhino, with a little man on its back.

And it does tessellate!  It gives a pattern in which the elenoceros repeats four times, right way up facing both ways, and then upside down facing both ways.

Illusion demos with animations, illusions and aesthetics, Tessellations

Tessellations

I love tessellations. Here’s quite a complicated example, with a transformation running across it, and an added graphic twist.

Want to try your own tessellations? There are software short-cuts you can use but to really get the hang of them, do them by hand, with a graphics package on a computer. (I use the graphics facility in a full version of Photoshop, but any capable graphics package should do the business. You will need to be fairly handy with it before you start doing tessellations, however). Or you can also really do them by hand, with tracing paper and pencil.

For an extended tutorial, see my tessellation tutorial, or visit another page with outstanding “how-to-do-it” demos.

Note added in March 2011!  If you are new to tessellations, first watch my later post with an animated demo of how tessellations work.

or for demos plus brilliant examples:

http://www.tessellations.org/mygallery16.htm (great examples)

For M.C. Escher’s tessellations see:
http://www.mcescher.com

Here’s my animated tessellation:

illusions and aesthetics, Tessellations

Tessellation Tutorial

Note added in March 2011!  If you’re new to tessellations, before tackling this post, first watch my later post with an animation of how tessellations work.

What is a tessellation?

Any regular pattern consists of identical areas, which repeat without overlaps or gaps. An obvious example would be tiles on a wall. However tiles are usually geometric shapes – rectangles or squares as a rule, though triangles or hexagons would be possible too. In a tessellation, the cells can have wiggly edges, but still fit together like jig-saw pieces.

If you try to make a pattern like that out of any old shape, you will either end up with gaps or overlaps:

To make cells that tessellate, you have to follow a recipe. There are a whole set of recipes, but to get an idea of how they work, take a look at just one.

Continue reading →