How do you see the figure above?  Make a judgment before you read on!

So what’s it about?

Continue reading →

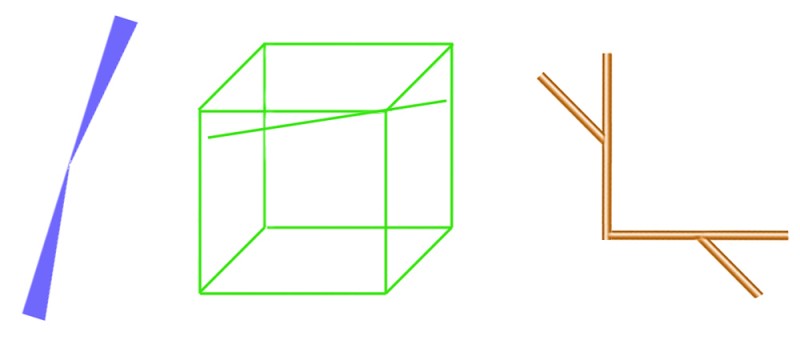
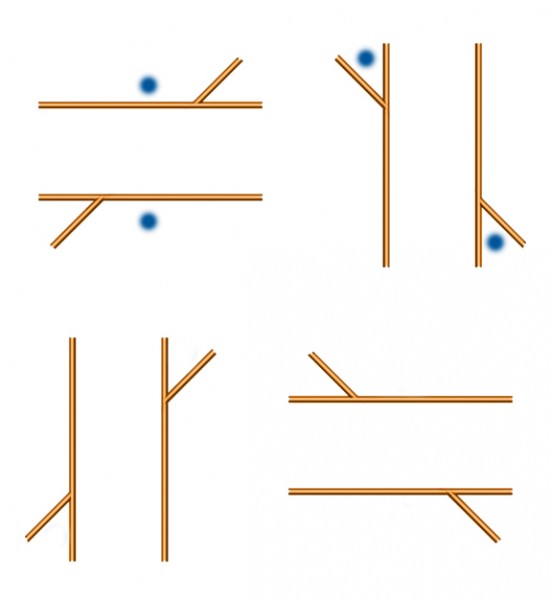This is another demo to see whether it’s true, as has often been claimed, that the Poggendorff illusion is much weaker when it’s seen in three dimensions.  To my eye, it’s not true:  in this lash-up of bits and pieces in my back yard, the illusion is still strong.  The long rod is straight as it passes behind the plank, but for me it looks just as decidedly misaligned either side of it when seen in 3D as when seen as a 2D photo.

To see the effect in three-dimensions, you’ll have to know how to view stereo picture pairs without a viewer, in what’s called “cross-eyed” mode.  If you don’t yet know that trick, you’ll find a tutorial at

http://spdbv.vital-it.ch/TheMolecularLevel/0Help/StereoView.html

But best to give it a miss if you have any problems with your eyes (apart from just being short sighted or colour blind, like I am) – or if viewing stereo pictures like these turns out to make you feel strange or queezy

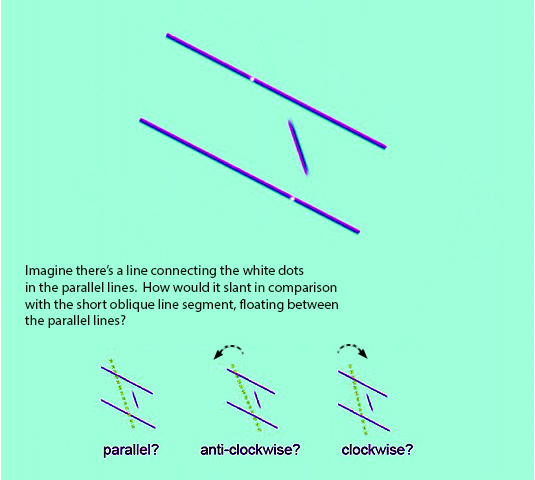
Many theorists have suggested that the Poggendorff illusion arises because we try to impose an inappropriate 3D interpretation on a 2D figure, which is the usual form in which the illusion is presented. It’s a very reasonable theory that might work in various ways, but as it happens, I just don’t think it’s true.

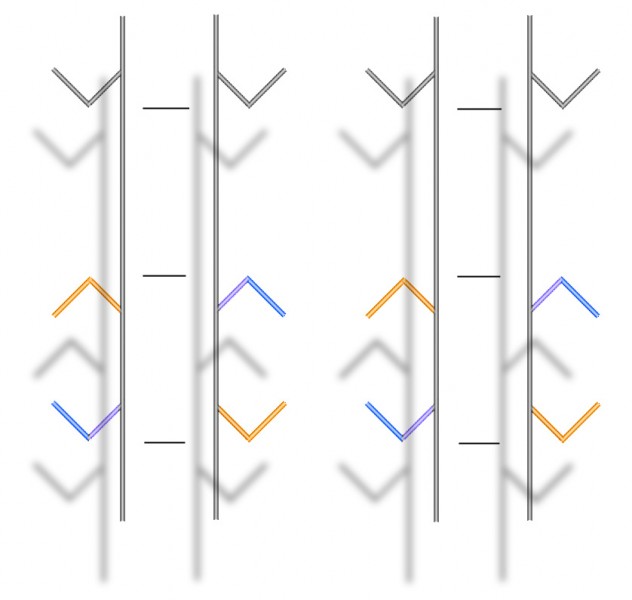
When we see the figure presented as a stereo image, as at the head of this post, so the theory goes, the illusion should vanish.

For more detail, see our earlier post on the Poggendorff illusion and depth processing:  http://www.opticalillusion.net/optical-illusions/the-poggendorff-illusion-and-depth-processing/

There’s another 3-D demo towards the end of that, but with the rod behind the plank in a plane parallel to that of the plank – in other words, not receding from us diagonally into the distance, like the rod in my back yard demo.  In this post, I wanted to check that the receding rod made no difference, and to my eye, it doesn’t, and nor does changing the orientation of the plank. The Poggendorff misalignment does look less in the lower pair, but that’s just because the plank that gets in the way in the lower images is at an angle where it looks much thinner.  It’s well-known that the illusion gets stronger as the gap between the rod segments gets wider.

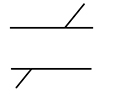
However, all this does not rule out a role for depth processing in the illusion.  Qin Wang and Masanori Idesawa have shown that when the illusion is presented in 3D with the test arms in front of the inducing parallel, illusion vanishes.  That’s a real challenge for the 2D theories.

Back in 1987 James Walker and Matthew Shank in the university of Missouri were doing a study of the Bourdon illusion. In some figures they devised for comparisons in their study they noticed a new effect, quite unrelated to their study. The figure upper left is a version of their chance discovery. The centre line is objectively horizontal, but can seem to rise slightly to the right. Walker and Shank tried the effect experimentally, and found it was indeed seen by a majority, but not all of their observers.  (Note for techies:  For a PDF of their article, input 1987 as year, the authors’ names plus Bourdon and contours as keywords on the Psychonomic Society search site).

The effect seems related to the Tolanski illusion, lower left: the gaps in the sloping lines are exactly level with one another, but the right hand one looks a touch higher. Generally, our judgments of horizontal or vertical across empty space between lines with a pronounced slope seem to get just a little rotated in the direction of the slope. The effect is even stronger for me with curved lines (as bottom right) than with straight ones. I’ve even found it in informal experiments with a number of observers as upper right, when vertically positioned target dots appear rotated towards the slope of blurred or broken slanting edges in which they are embedded.

But in my version of the figure, upper left, we can also see the Poggendorff effect at work, (according to me at least). Look at the two outer, nearly horizontal arms. They are exactly aligned, but to my eye the right hand one looks higher than the left hand one. That’s just the result we would get if we deleted the middle three pairs of lines, to end up with opposed obtuse angles, in what is sometimes called an obtuse angle Poggendorff figure.

Do the Tolanski and Pogendorff illusions share a mechanism, or do we see in the top left figure both the rotation of the horizontal line, and the misalignment of the outer arms, arising by chance from different processes in the brain? We can’t yet be sure, but I reckon the same processes are most probably at work, and are to do with projecting orientation and alignment judgments across figures with powerfully competing axial emphasis. The Tolanski and Poggendorff figures present a sort of reciprocal pairing: with Tolanski figures judgments of vertical or horizontal are compromised in a figure with a dominant slant, whereas in classic versions of the Poggendorff illusion judgments of oblique alignment are rotated between vertical or horizontal lines.

Here are three rather subtle illusions, each showing bent lines. In Bourdon’s illusion, to the left, the straight left hand edge looks bent. In Humphrey’s figure, centre, the straight, loose line touching the corner of the cube looks bent. And in the figure to the right, the straight line interrupted by the corner looks bent. I don’t think we really understand any of these illusions, and they are not very dramatic, so you don’t see them often. When someone does puzzle them out, for sure they’ll be a key to subtle ways the brain works. There’s probably a different explanation for each. For example, both the left and middle figures show a bent line that is the backbone of two triangles meeting at a point, so you might think, hello hello, we’re getting somewhere. But then you notice that the lines bend in different directions in relation to the triangles each illusion.

If you like to tangle with the technicalities, there are learned studies of the Bourdon illusion and the corner figure, though unfortunately, you’ll only get an abstract of the articles on those links, unless you are in a university library where they subscribe to the journals. And you won’t find much on Humphrey’s figure anyway, it’s seriously obscure.

Here’s a bit more on the corner figure  ….

Continue reading →

This is a stereo picture-pair, but you can see what’s happening here without having to view the images in 3D if you prefer.  However,  if you’ve not got the knack, and would like to practice on this post, here’s how.  Hold up a pen about in the middle, between the two pictures, and about five inches from your eyes (careful!).  If you now try to focus on the tip of the pen, you’ll notice that the blurry image of the figure has doubled.  Now move the pen-tip away from your eyes, and notice that the two blurry middle images of the figure are beginning to overlap.  Once they overlap (probably when the pen-tip is something like ten inches away from your face), see if you can get them to overlap exactly, and then come into focus.  If that doesn’t work, try this great tutorial on another site. Or try our earlier post about stereo picture pairs.

If you’ve got it, you should see the parallel vertical bars and their attachments floating in front of a surface with their shadows thrown on it. You’ll see the same if you view the image normally, but not with the illusion of 3D.  So what’s going on?

It’s a much stronger version of some paradoxical effects I showed in an earlier post.  The tips of the arrowheads are all objectively exactly the same distance apart, as indicated by the horizontal lines aligned with them in between the vertical bars.  But that’s not how they appear if you look at the arrowheads:  the inward pointing arrows look much further apart than the outward pointing ones.  (That’s the Mueller-Lyer illusion).  But now check out the lower, coloured arrowheads.  The coloured arms that contact the vertical bars are objectively aligned, but appear not to be – the upper arm in each case seems shifted a bit upward, and the lower arm a bit downward.  (That’s the Poggendorff illusion).  For the arms to appear out of alignment like that, you’d imagine the arrowheads must move further apart.  But that’s exactly the opposite of what the Mueller-Lyer illusion is making them seem to do.

Continue reading →

This is Morinaga’s paradox – two illusions in one, but two illusions that contradict one another. First note the vertical alignment of the arrow points. Don’t the tips of the inward pointing arrowheads, top and bottom, appear to be located just a little further inwards than the tips of the middle, outward pointing arrowheads? That could only be right if the horizontal space between the tips of the (top and bottom) inward pointing arrowheads was slightly less than the space between the tips of the (middle) outward pointing ones. But that’s not how it looks. The inward pointing arrowheads look further apart than the outward pointing ones.

In reality both judgments, of vertical alignment and of the horizontal gaps, are illusions.  The tips of the arrows are perfectly aligned vertically, and the horizontal gaps between the three sets of arrowheads are all exactly the same. That last effect is a version of the Muller-Lyer illusion.

Continue reading →

One of the most obstinately puzzling illusions is Poggendorff’s, in which a slanting line interrupted by a gap no longer looks aligned. For over a century specialists have been unable even to agree whether it arises from 2D properties of the image, or as a result of attempts by the brain to interpret the configuration as 3D. Papers written a hundred years ago treat the problem in very much the same terms as we do today. I’m betting on 2D (I argue for that on another, website devoted to the Poggendorff illusion). It’s not likely my speculations are spot on, and they may well not even be in the right direction. But read on here if you’d like to see demonstrations that show why I don’t think depth processing can be the answer.

Continue reading →