Category Archives: Optical Illusions

Geometric illusions, Optical Illusions

Competing illusions

 

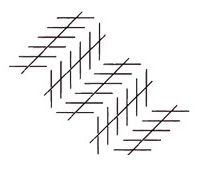
Here’s a rather subtle effect. It’s a competition underway, when the Zollner illusion is seen embedded in a staircase. In the staircase lower left, where two of the long lines are either side of the outside edge of a step (in other words like lines a and b here, on the sides of a convex step), the lines seem to get further apart with distance, as they would in a normal presentation of the Zollner illusion. But wherever on that lower left stair the lines are like b and c here, either side of the inner edge of a step, (so on a concave step), they tend to look much more parallel. In a normal version of the illusion, as below, the equivalent long lines appear to get closer together to the right.

Want to know more?

Continue reading →

Geometric illusions, Optical Illusions, The Poggendorff Illusion

The Poggendorff Illusion and depth processing

2 Comments


One of the most obstinately puzzling illusions is Poggendorff’s, in which a slanting line interrupted by a gap no longer looks aligned. For over a century specialists have been unable even to agree whether it arises from 2D properties of the image, or as a result of attempts by the brain to interpret the configuration as 3D. Papers written a hundred years ago treat the problem in very much the same terms as we do today. I’m betting on 2D (I argue for that on another, website devoted to the Poggendorff illusion). It’s not likely my speculations are spot on, and they may well not even be in the right direction. But read on here if you’d like to see demonstrations that show why I don’t think depth processing can be the answer.

Continue reading →

Geometric illusions, Optical Illusions, Size-constancy effects

Paradoxical Size Constancy

Size constancy is the term for our tendency to see distant objects as larger than they are. So the far end of a shape with parallel sides looks wider than the near end. (See the earlier post on The Wonky Window). It seems to be such a basic feature of vision that it can give rise to amazing effects.  In the photo, first note note that the “sculpture” is impossible! All four blocks are receding from us, so they could only connect up in real space as a bendy snake. Instead they join up in an impossible, ever-receding, endless loop.  (See the earlier post on M.C.Escher’s Waterfall for how that kind of impossible figure works). Here the endless loop leads to a paradox, thanks to size constancy. The distant end of each block seems wider than the near end, and yet at the same time seems to be exactly the same size as the apparently smaller, near end of the next block. Measure the sides of the blocks and you’ll find them parallel. It’s one of many demonstrations that perceptual space is not always geometrically consistent, (or it can be non-Euclidean, as the specialists put it).

 

I located my impossible sculpture in a deeply receding space because that makes the effect just a bit stronger.

Update January 2010: How could I have overlooked this?  The stripes I’ve added to these blocks will be enhancing the effect of divergence by adding the chevron illusion to the size-constancy effect.  The chevron illusion was first reported 500 years ago, by French writer Montaigne, as related in Jaques Ninio’s book on illusions, page 15.  The chevron effect is a special case of the illusion later re-discovered a bit over a century ago as the Zollner illusion.  Some specialists would say both effects depend on the brain’s attempts to make sense of figures as shapes in space.  I suspect that’s true of the size-constancy effect, but that the chevron effect is 2D, pattern driven.  That seems supported by the observation that whilst in the picture above the chevron and size-constancy effects are acting in consort, they can also oppose one another, reducing the effect of divergence.

Read on for more on size-constancy.

Continue reading →

Ambiguous images, Optical Illusions

An Ambiguous Skull-Mask Illusion

Is this a picture of a mask looking at a skull it’s holding up for inspection, or vice versa?

I got the idea from a print by Picasso, Young man with mask of a bull, faun and profile of a woman. There’s a copy in the Art Gallery of New South Wales in Sydney, and you can see it by calling up,

http://www.artgallery.nsw.gov.au/collection/simple_search

search for Picasso, scroll down the results and you’ll find it!

Ambiguous images, Illusion demos with animations, Optical Illusions

Revolving Heads

3 Comments

Heads that present one character one way up and another when rotated have been favorite illusions for over a century. Here are two heads from a cartoon story I devised about a boy who gets stuck in a weird hotel. The receptionist and chef, (Mr. and Mrs. Turner …. ) seem OK at first, but then transform into two sinister old men when their heads rotate.

For an animation of Mr. and Mrs. Turner see below:

There are loads of great rotating heads at:

http://members.lycos.nl/amazingart/E/6.html Rotating Heads

Impossible worlds (inc. staircases), Optical Illusions

Optical Illusion Cartoon Story

For years I’ve wished someone would make an animated cartoon in which the events depend on the kind of visual transformations we see in many illusion pictures. It won’t be easy. Salvador Dali loved effects of these kinds, and helped sketch out a scheme for a Disney movie (though not one with a real storyline) in 1945/6. It’s called Destino. It didn’t get made, until Disney’s nephew Roy Disney made a version in about 2000. I don’t think it was so successful, but it was a fascinating chance to see what works, and what is less successful when animated. Take a look at a trailer and decide,

http://www.youtube.com/watch?v=iO1ghQFSXro

I reckon Goo-Shun Wang’s wonderful, recent animation of a character trapped on an Escher-style, never-ending staircase is far more successful:

http://www.moillusions.com/2007/04/halluciis-problem-illusion-video.html

To explore the kind of effects I think might work in a narrative, I devised a couple of still-picture cartoon stories. Here’s a pair of frames from one you can view on the www, in which the characters are almost trapped on another never-ending staircase, when a spiral stair suddenly transforms:

Check out the whole thing at:

http://www.Opticaloctopus.com

it also includes loads of hints on drawing illusion pictures.

Geometric illusions, Optical Illusions

(Not so) Geometric Illusions

Many of the illusions in popular books are geometric ones, in which lines that are really parallel look wonky, or lines that are aligned seem not to be. Most of these figures were discovered by German researchers, a hundred to a hundred and fifty years ago. But how geometric do they have to be? With graphics packages it’s easy and fun to explore. Here are versions of two famous illusions, one showing apparent divergence where the other presents convergence, against the same “zebra skin” background.

Continue reading →