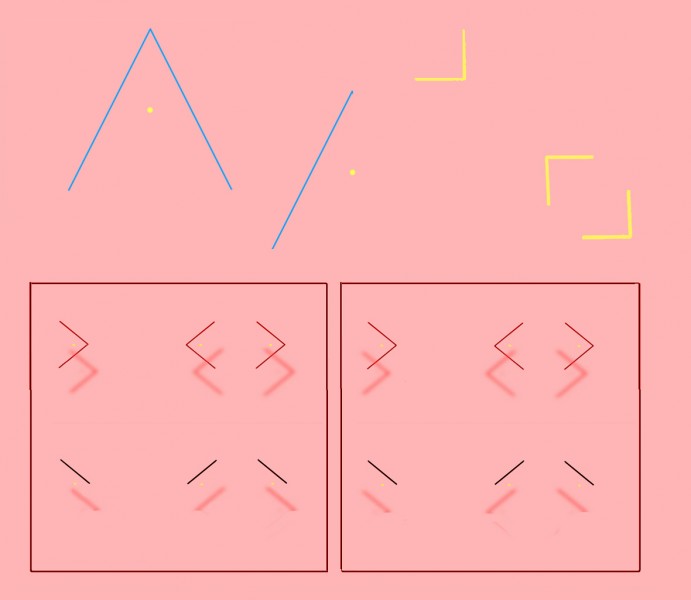
Top left is one of the simplest of all illusions.  The yellow dot is just half way up the vertical height of the triangle, but looks decidedly nearer to the apex. The effect was reported over a century ago, and has been named for its original researchers the “Thiery-Wundt illusion” by recent experimenters Ross Day and Andrew Kimm.  A consensus in recent years has been that we are hard-wired to home in on the “centre of gravity” of the triangle, the point at which three lines bisecting the three angles would meet.  The centre of gravity is a bit lower down than the half-way point of the vertical height of the triangle.  So maybe, the theory goes, we tend to take the centre of gravity as a default central reference point, and so we see the vertical centre point as if shifted a bit towards the apex.  But that can’t be the whole story, researchers Day and Kimm point out, because the effect is still there when the figure is reduced to just one oblique angle side, as centre top in the figure.  In fact, in their experiments, the effect was measured as even stronger that way. So the illusion may look simple, but more than a hundred years after its debut, we’re still basically guessing what’s going on.

Whatever is afoot, it’s probably also involved in the Mueller-Lyer illusion, in which the gap between two inward pointing arrowheads looks larger than an identical gap between two outward pointing ones.  I’ve shown that in 3D in the figure, for viewers who have the knack of so-called “cross-eyed” 3D viewing, without a viewer.  (If that’s new to you, and you want to get the knack, search on Google or try this site – though give it a miss if you have vision problems). But you can see the Mueller-Lyer effect perfectly well in 2D, and for a full discussion of the two illusions, Thiery-Wundt and Mueller-Lyer, if you have access to a research library, see Day and Kimm’s original research paper.  Or for just a bit more ….

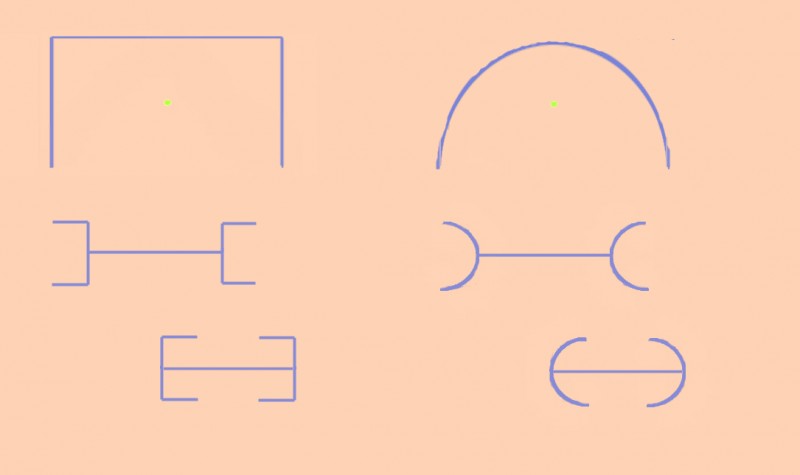
I’ve shown Mueller-Lyer as a flat figure hanging in 3D space partly because it’s more fun that way, but also because I reckon doing so undermines one of the traditional explanations for the illusion – that it arises from our attempts to interpret the figure as an array of lines in space.  According to that proposal, the inward pointing arrows look like a corner in perspective receding away from us, and so further away than the outward pointing pair, which look like a corner jutting out towards us.  The space between the apparently more distant, inward-pointing arrowheads then looks larger, it is suggested, because of the size-constancy effect.  (Or for more on size-constancy, there’s a whole category of posts in the list to the right).

I don’t think that can be right.  When the Mueller-Lyer figures are shown in 3D, but so that as here they look flat in space, the illusion is just as strong. Well, OK, some would say the flatness is irrelevant, because the effect is a left-over from evocation very early in visual processing of possible spatial schemes in the array of lines, evocations that rapidly fell by the wayside, giving way to the percept of a flat figure, but leaving the illusion behind as a kind of ghost.  But then look at the variant of the illusion upper right in my figure, where it is rotated 45 degrees.  With the angles also now right angles, all the lines are vertical or horizontal, so that even early in visual processing there would be no consistent perspective cues.  Yet the illusion persists.

So maybe it is related – somehow – to whatever is going on in Thiery-Wundt.  Day and Kimm show a number of variations on the Thiery-Wundt illusion, including examples like the ones in this figure.  They found the effect still there, but a bit tenuous, with the rectangular figure, and just a bit stronger with the oval.  But that does fit suggestively well, at least to my eye, with the strength of effect in related Mueller-Lyer figures.  However, I wonder if the Thiery-Wundt illusion might also have something to do with apparent position shifts associated with the Tolanski illusion.  That couldn’t be the case with the rectangular figure, but maybe that’s why it’s so weak.  However the demos I’ve tried so far, though a bit suggestive, are far from compelling.