Top left is one of the simplest of all illusions.  The yellow dot is just half way up the vertical height of the triangle, but looks decidedly nearer to the apex. The effect was reported over a century ago, and has been named for its original researchers the “Thiery-Wundt illusion” by recent experimenters Ross Day and Andrew Kimm.  A consensus in recent years has been that we are hard-wired to home in on the “centre of gravity” of the triangle, the point at which three lines bisecting the three angles would meet.  The centre of gravity is a bit lower down than the half-way point of the vertical height of the triangle.  So maybe, the theory goes, we tend to take the centre of gravity as a default central reference point, and so we see the vertical centre point as if shifted a bit towards the apex.  But that can’t be the whole story, researchers Day and Kimm point out, because the effect is still there when the figure is reduced to just one oblique angle side, as centre top in the figure.  In fact, in their experiments, the effect was measured as even stronger that way. So the illusion may look simple, but more than a hundred years after its debut, we’re still basically guessing what’s going on.

Whatever is afoot, it’s probably also involved in the Mueller-Lyer illusion, in which the gap between two inward pointing arrowheads looks larger than an identical gap between two outward pointing ones.  I’ve shown that in 3D in the figure, for viewers who have the knack of so-called “cross-eyed” 3D viewing, without a viewer.  (If that’s new to you, and you want to get the knack, search on Google or try this site – though give it a miss if you have vision problems). But you can see the Mueller-Lyer effect perfectly well in 2D, and for a full discussion of the two illusions, Thiery-Wundt and Mueller-Lyer, if you have access to a research library, see Day and Kimm’s original research paper.  Or for just a bit more ….

Continue reading →

This is a third look at the Shepard’s tables illusion. If you didn’t see the earlier posts, you might like to get up to speed on the illusion by scrolling down two posts to an animated demo. The two pairs of table-tops in these views are absolutely identical, and within each pair the two lozenge shapes are identical except that one is seen short end on, and the other wide side on. However, they don’t look identical. Most dramatically, the lower table in the left hand image looks much longer and thinner than the upper table. But we don’t see that stretch into depth in the identical pair of table-tops in the right hand image. They look quite different, just because the tables are shown tipped over.

The stretch-into-depth of the lower table in the left hand image is a kind of size-constancy effect. But the tables also show a more familiar kind of size constancy effect.  Check out the blue lines in the left hand image (left edge of the upper table and alignment of the bottom of the table legs). Those blue lines are parallel, but to my eye they look as if they get wider apart with distance.

In the left hand image, to my eye, only the blue lines show apparent divergence with distance. The horizontal edges (yellow) and the vertical table legs (red edges) stay parallel for me. But in the right hand picture, just tipping the tables over makes all three pairs of coloured edges appear to diverge with distance. The effect may not be very strong. It’s easier to see in bigger versions of the pictures, so I’ll add those in in what follows, where I want to pose a question: are the differences between the table-tops as seen upright and tipped over only to do with how we see pictures, or are they a clue to how we see more generally?

Continue reading →

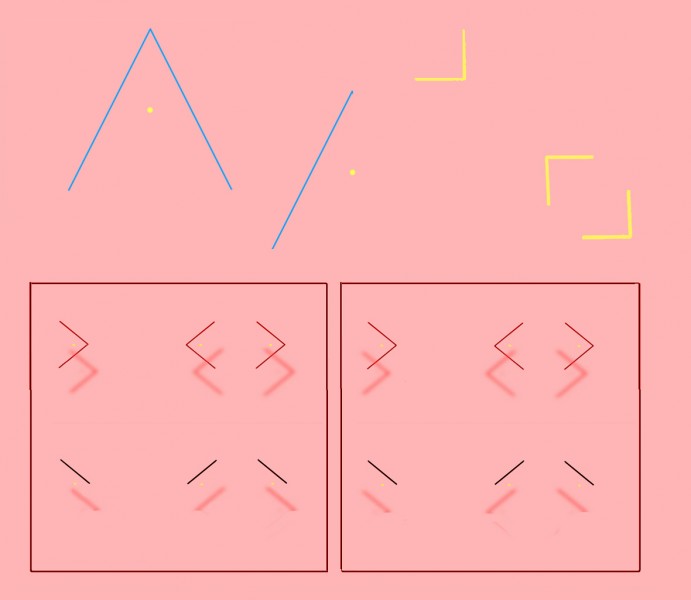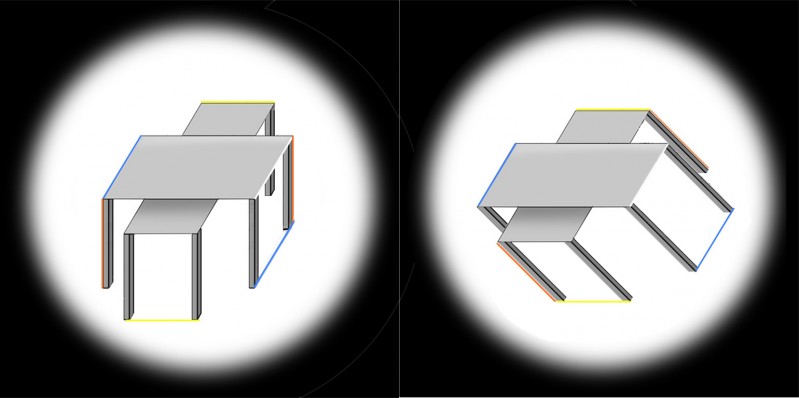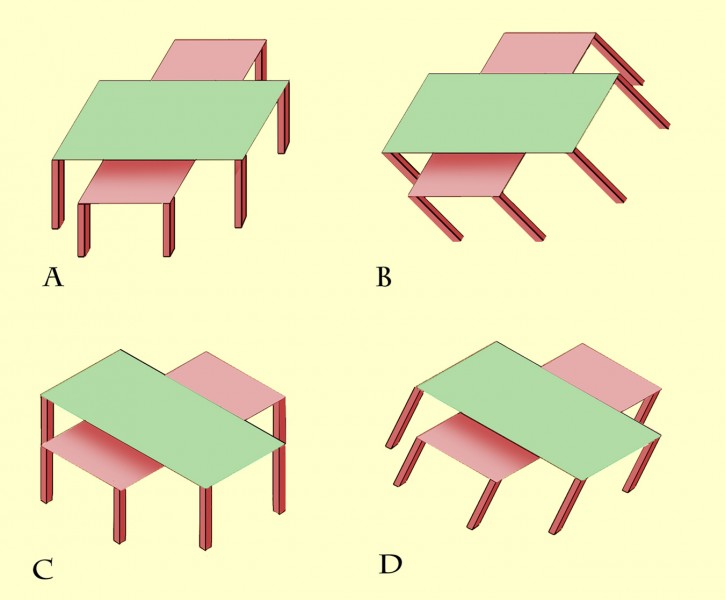
The previous post presented an animation of Shepard’s Tables. If you didn’t see that, you might want to check it out first (scroll down to the previous post) to get the basics of the illusion. This new version of the illusion, with nested tables, follows the pattern: all eight of the lozenge shaped table-tops are identical in shape, but the more that a lozenge is seen with its long edge parallel to the line of sight, the more it looks long and thin as it stretches into the distance. The more it’s seen short edge parallel to the line of sight, the more it looks wide and stumpy.

Describing the illusion that way may explain a puzzling variant of Shepard’s Tables, recently reported by Lydia Maniatis, as mentioned in the previous post. As the problem appears in these nested tables, at B the edges of the table-tops that are horizontal on the screen must be receding into depth, and yet they don’t show the dramatic illusion of a stretch into depth that we see in the edges receding into distance at A. Why not?

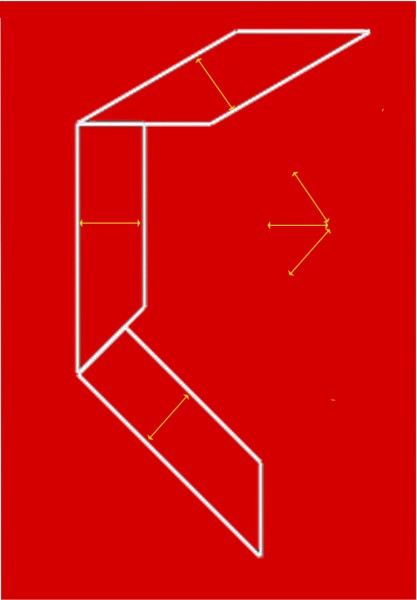
Isn’t it a question of perspective? At A the horizontal table edges are represented as if seen head on, parallel to the image plane – the plane at right angles to our line of sight. The table edges that are oblique on the screen at A must therefore be extending into depth in the most extreme way, parallel to the line of sight and at right angles to the image plane. Seen like that, depth effects are maximised. At B, no edges are aligned with the image plane, and all the edges, even the ones that are horizontal on the screen, are receding at 45 degrees to the line of sight. That’s a much less extreme recession into depth. So although the table edges that are objectively horizontal on the screen at B are receding, they don’t show as much illusory stretch into depth as the receding edges in A. 

Lydia Maniatis observation raises a general point that’s really interesting – the way that appearances can depend on what we mean by “up”.

Continue reading →

Here’s another illusion only recently reported, by Daniella Bresanelli and Manfredo Massironi of the Universities of Padua and Verona.  Look at the three shapes, and most people seem to see the bottom one as thinnest, judging width at right angles to the long edges, the middle one as a bit fatter, and the top one as widest of all (still judging width at right angles to the long edges).  In fact, they’re all the same width, and the two bottom shapes are also identical, just rotated in relation to one another.

What’s going on?  If you devour technical articles like snacks, see Bressanelli and Massironi’s paper.  Otherwise …

Continue reading →

Size constancy is the term for our tendency to see distant objects as larger than they are. So the far end of a shape with parallel sides looks wider than the near end. (See the earlier post on The Wonky Window). It seems to be such a basic feature of vision that it can give rise to amazing effects.  In the photo, first note note that the “sculpture” is impossible! All four blocks are receding from us, so they could only connect up in real space as a bendy snake. Instead they join up in an impossible, ever-receding, endless loop.  (See the earlier post on M.C.Escher’s Waterfall for how that kind of impossible figure works). Here the endless loop leads to a paradox, thanks to size constancy. The distant end of each block seems wider than the near end, and yet at the same time seems to be exactly the same size as the apparently smaller, near end of the next block. Measure the sides of the blocks and you’ll find them parallel. It’s one of many demonstrations that perceptual space is not always geometrically consistent, (or it can be non-Euclidean, as the specialists put it).

I located my impossible sculpture in a deeply receding space because that makes the effect just a bit stronger.

Update January 2010: How could I have overlooked this?  The stripes I’ve added to these blocks will be enhancing the effect of divergence by adding the chevron illusion to the size-constancy effect.  The chevron illusion was first reported 500 years ago, by French writer Montaigne, as related in Jaques Ninio’s book on illusions, page 15.  The chevron effect is a special case of the illusion later re-discovered a bit over a century ago as the Zollner illusion.  Some specialists would say both effects depend on the brain’s attempts to make sense of figures as shapes in space.  I suspect that’s true of the size-constancy effect, but that the chevron effect is 2D, pattern driven.  That seems supported by the observation that whilst in the picture above the chevron and size-constancy effects are acting in consort, they can also oppose one another, reducing the effect of divergence.

Read on for more on size-constancy.

Continue reading →

(re-draft August 2016) The right hand upper window is leaning the wrong way, which is wonky for a start, but it’s not quite as wonky as it looks. It’s really identical to the window on the left and only seems to lean over more.  What’s going on?

Continue reading →